research

Why a morfogenetic field theory? Motivation

In 1976 Lynn and Tucker studied the biological mechanisms responsible for defining organelles position inside cells. This class of studies were the observational and experimental support of the ‘morphogenetic field’ notion. In the present paper [18] we studied the morphogenetic field evolution yielding from an initial population of cells to different unicellular organisms as well as specialized eucariotic cells. Both types of cells were represented as Julia sets and Pickover biomorphs, simulating Darwinian natural selection with a simple genetic algorithm.

A morphogenetic field has been defined as a plane A with points representing the locations where cells are differentiated or sub-cellular components (or organelles) organized, being the plane A an tissue or cell, respectively. The region A representing the morphogenetic field assumes two X, Y orthogonally diffusing chemicals modeled as the real and imaginary components on the complex plane where a biomorph (a cell and its organelles) is differentiated and evolved. We found that Pickover cells show a higher diversity of size and form than those populations of cells evolved as Julia sets. Another novelty is the way that cellular organelles and cell nucleus fill the cell depending on cell definition as Julia set or Pickover biomorph.

Our findings [18] support the existence of some attractors representing the functional and stable form of a cell. The morphogenetic field is attracted towards one or another attractor depending on the environment modeled by a particular fitness function. The model promotes the view of Waddington, Goodwin and D’Arcy Thompson that considers organisms as dynamical systems that evolve through a ‘master plan’ of transformations.

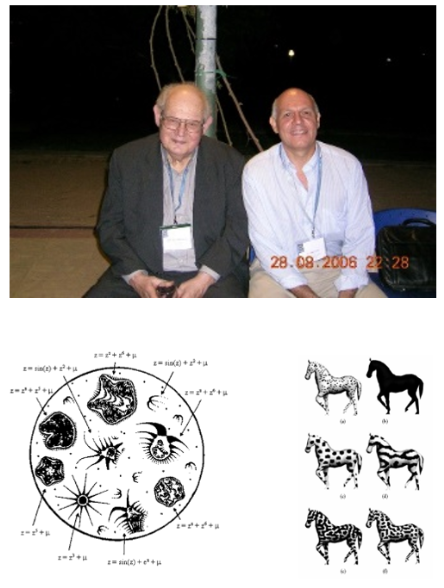
Modeling the zebra strip pattern

One of the classical problems of morphogenesis is to explain how patterns of different animals evolved resulting in a consolidated and stable pattern generation after generation. In this paper [16] we simulated the evolution of two hypothetical morphogens, or proteins, that diffuse across a grid modeling the zebra skin pattern in an embryonic state, composed of pigmented and nonpigmented cells. The simulation experiments were carried out applying a  genetic algorithm (Transl.: Spanish) to the Young cellular automaton: a discrete version of the reaction-diffusion equations proposed by Turing in 1952. In the simulation experiments we searched for proper parameter values of two hypothetical proteins playing the role of activator and inhibitor morphogens. Our results [16] show that on molecular and cellular levels recombination is the genetic mechanism that plays the key role in morphogen evolution, obtaining similar results in the presence or absence of mutation. However, spot patterns appear more often than stripe patterns on the simulated skin of zebras. Even when simulation results are consistent with the general picture of pattern modeling and simulation based on the Turing reaction-diffusion, we conclude that the stripe pattern of zebras may be a result of other biological features (i.e., genetic interactions, the Kipling hypothesis).



Evolving biomorphs with a simple genetic algorithm

Genetic algorithms are stochastic optimization procedures based on Darwinian natural selection. This optimization technique uses genetic operators, thus procedures inspired in the genetic mechanism observed in populations such as crossover or recombination (combination of two solutions) and mutation (random change of a solution). At present, the application of genetic algorithms to fractal is a common approach in applied and theoretical research. In this paper [18] a simple version of a genetic algorithm was applied to evolve a population P(t), being P(t) a population of 'cells' or Pickover biomorphs represented each one by a complex function. The genetic algorithm was defined as follows:

1. Choose initial population P(0) of biomorphs.
2. Evaluate the fitness of each biomorph in the population P(t).
3. Select the best-fitness biomorphs to reproduce.
4. Breed a new generation through crossover and mutation and give birth to offspring.
5. Replace worst ranked part of population with offspring.
6. Until <terminating condition>

Top photo .- Benoit Mandelbrot and me attending at the International Congress of Mathematics, Madrid 2006.

Bottom .- Evolving (Left) biomorphs and (Right) zebra skin pattern

Biomorphs were evolved [18] in different environments (or under different fitness functions,  see Fitness functions) to one of the following cellular classes:

• Class I. Ancient cells without cell nucleus and mitochondrion, a thin membrane and watery environment.
• Class II. Is a kind of cells similar to class I excepting the cells have mitochondrion.
• Class III. Cells have small size and a large membrane.
• Class IV. Small and round cells, with cell nucleus and mitochondrion, having a thin membrane.
• Class V. Cells similar to class III, excepting the cells have a larger size.
• Class VI. Large and round cells, with cell nucleus and organelles.
• Class VII. Large cells with radial symmetry, having cell nucleus and organelles.
• Class VIII. Aligned rectangular cells, with axial symmetry, developing layers or tissues.
• Class IX. Specialized in communication cell-to-cell (i.e. neurons). Membrane with a large surface, ‘synapses’.
• Class X. ‘Feed cells’, specialized in absorption of nutrients (i.e. intestinal cells) from environment.
• Class XI. Cells specialized in the transport of substances, without cell nucleus (i.e. red blood cells).

The beauty of the mammalian vascular system

Beauty is a characteristic of objects that provides a perceptual experience of pleasure. In nature, aesthetic appreciation thereof has given rise to the mathematical search for good series (e.g. the Fibonacci series) and proportions (e.g. the Golden proportion) as important elements of beauty. In 1928 the mathematician George David Birkhoff introduced a formula for aesthetic measurement of an object. Birkhoff equation defines the aesthetic value as the amount of order divided by the complexity of the product. These two features can be measured easily in poetry, music, painting, architecture, etc. In the fine arts, it is the artist who manipulates both these features, but how does nature manage order and complexity in living organisms or their parts? Here we show [10c] how Birkhoff equation, applied to the mammalian vascular system of eight representative animals, results in new insights into the organization of the animal vascular system. In a colaboration with Julio Gil (author of this very original idea) and cols. (Department of Anatomy, Embryology and Animal Genetics, University of Zaragoza, Spain) we found [10c] that order and complexity are highly correlated in the mammalian vascular system (R2=0.9511). Accordingly, in nature both features are not independently managed in the manner of artists. We found significant differences among the Birkhoff aesthetic values in the mammalian arterial system, whereas no such differences exist in the venous system. We anticipate our approach to be useful in the study of morphogenesis and evolution of tree-like structures, employing the Birkhoff aesthetic value as a simple tool for conducting such studies.